
 |
|
| Главная | Деятельность | Мероприятия | Школа юных | Работа с учителями | | |
| Мероприятия » Международный математический Турнир Городов » Задачи осеннего тура - Основной вариант | |
ДВАДЦАТЬ СЕДЬМОЙ ТУРНИР ГОРОДОВ |
| Баллы | Задачи |
4 |
1. Четырех мудрецов одного за другим посадили на скамью так, что первый не видит ни одного из остальных трех, второй – видит только первого, третий – первого и второго, четвертый – трех первых. Им показали 3 белые и 4 черные шляпы, попросили закрыть глаза и надели на головы какие-то из этих шляп. Затем мудрецы открыли глаза. Судья спросил у четвертого: «Может ли он сказать, какого цвета на нем шляпа?». Тот сказал, что нет. Третий и второй на такой же вопрос тоже ответили отрицательно (отвечали они один за другим). И только первый, услышав, все ответы сказал: «Я знаю, какая шляпа у меня на голове!» Объясните, как он смог догадаться. |
|
2. Палиндром – это натуральное
число, которое читается одинаково слева направо и справа налево (например, 1
или 343 или 2002 палиндромы, а 2005 – нет).
а) Найдется ли 25 пар вида (n, n + 110), где оба числа – палиндромы? б) Найдется ли 2005 пар вида |
3 3 |
3. а) У Карлсона есть 27 банок с вареньем. В банках находится 1,
2, 3, …, 27 литров варенья соответственно. На завтрак Карлсон
может съесть по одинаковому целому числу литров варенья из любых двух из этих
банок. Докажите, что Карлсон может действовать так,
чтобы за некоторое количество
завтраков съесть все варенье. б) Может ли Карлсон съесть все варенье в случае, если вначале было 29 банок, в которых было 1, 2, …, 29 литров варенья? |
| 2 3 |
4. а) Разместите в кружочках 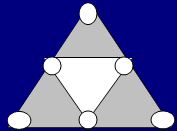 числа 1, 2, 3, 4, 5, 6 так, чтобы
сумма
чисел в вершинах каждого заштрихованного
треугольника была простым числом. (Укажите хотя бы один вариант.)
числа 1, 2, 3, 4, 5, 6 так, чтобы
сумма
чисел в вершинах каждого заштрихованного
треугольника была простым числом. (Укажите хотя бы один вариант.)
б) Может ли при этом сумма чисел в вершинах четвертого маленького треугольника тоже быть простым числом? в) Можно ли в пункте а) так расставить числа, что все суммы – различные простые числа? |
7 |
5. Играют двое. Игровое поле – строка из 101 клетки, между которыми в некотором порядке стоят 50 плюсов и 50 минусов. Кроме этого, имеются карточки с числами от 1 до 101. Первый из игроков берет карточки одну за другой в некотором порядке, а второй указывает, на какую клетку в строке положить очередную карточку. Когда вся строка заполнена, вычисляется значение полученного выражения. В итоге второму игроку необходимо получить счастливое число 77. Может он этого добиться, или первый игрок способен ему помешать? |
7 |
6. На каждой клетке шахматной доски вначале стоит по ладье. Каждым ходом можно снять с доски ладью, которая бьет нечетное число ладей. Какое наибольшее число ладей вы сможете снять? Укажите соответствующий вариант. Может быть, вам удастся показать, что большего числа ладей снять нельзя. (Ладьи бьют друг друга, если они стоят на одной вертикали или горизонтали и между ними нет других ладей). |
8-9 классы
| Баллы | Задачи |
3 |
1. Палиндром – это натуральное число, которое читается одинаково слева направо и справа налево (например, 1, 343 и 2002 палиндромы, а 2005 – нет). Найдется ли 2005 пар вида (n, n + 110), где оба числа – палиндромы? |
5 |
2. Продолжения сторон AB и CD выпуклого четырехугольника ABCD пересекаются в точке K. Известно, что AD = BC. Пусть M и N – середины сторон AB и CD. Докажите, что треугольник MNK тупоугольный. |
6 |
3. На каждой клетке шахматной доски вначале стоит по ладье. Каждым ходом можно снять с доски ладью, которая бьет нечетное число ладей. Какое наибольшее число ладей можно снять? (Ладьи бьют друг друга, если они стоят на одной вертикали или горизонтали и между ними нет других ладей). |
4 |
4. По краю многоугольного стола ползут два муравья.
Все стороны стола длиннее 1 м, а расстояние между муравьями всегда ровно 10
см. Сначала оба муравья находятся на одной из сторон стола. а) Пусть стол выпуклый. Всегда ли муравьи смогут проползти по краю стола так, чтобы в каждой точке края побывал каждый из муравьев? б) Пусть стол не обязательно выпуклый. Всегда ли муравьи смогут проползти по краю стола так, чтобы на краю не осталось точек, в которых не побывал ни один из муравьев? |
7 |
5. Найдите наибольшее натуральное число N, для которого уравнение 99x + 100y + 101z = N имеет единственное решение в натуральных числах x, y, z . |
8 |
6. У Карлсона есть 1000 банок с вареньем. Банки не обязательно одинаковые, но в каждой не больше, чем 1/100 часть всего варенья. На завтрак Карлсон может съесть поровну варенья из любых 100 банок. Докажите, что Карлсон может действовать так, чтобы за некоторое количество завтраков съесть все варенье. |
10-11 классы
| Баллы | Задачи |
3 |
1. При каких n найдутся такие различные натуральные
числа 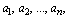 что сумма
что сумма 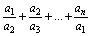 – целое число?
– целое число?
|
2 3 |
2. По краю многоугольного стола ползут два муравья.
Все стороны стола длиннее 1 м, а расстояние между муравьями всегда ровно 10
см. Сначала оба муравья находятся на одной из сторон стола. а) Пусть стол выпуклый. Всегда ли муравьи смогут проползти по краю стола так, чтобы в каждой точке края побывал каждый из муравьев? б) Пусть стол не обязательно выпуклый. Всегда ли муравьи смогут проползти по краю стола так, чтобы на краю не осталось точек, в которых не побывал ни один из муравьев? |
5 |
3. На каждой клетке шахматной доски вначале стоит по ладье. Каждым ходом можно снять с доски ладью, которая бьет нечетное число ладей. Какое наибольшее число ладей можно снять? (Ладьи бьют другдруга, если они стоят на одной вертикали или горизонтали и между ними нет других ладей). |
6 |
4. На окружности расставлено несколько положительных чисел, каждое из которых не больше 1. Докажите, что можно разделить окружность на три дуги так, что суммы чисел на соседних дугах будут отличаться не больше, чем на 1. (Замечание. Если на дуге нет чисел, то сумма на ней считается равной нулю.) |
7 |
5. Дан треугольник ABC, AA1, BB1 и CC1 – его биссектрисы. Известно, что величины углов A, B и C относятся как 4:2:1. Докажите, что A1B1=A1 C1. |
8 |
6. На доске можно либо написать две единицы, либо стереть любые два уже написанных одинаковых числа n и написать вместо них числа n + 1 и n – 1. Какое минимальное количество таких операций требуется, чтобы получить число 2005? (Сначала доска была чистой.) |
| Главная | Деятельность | Мероприятия | Школа юных | Работа с учителями | | |
© 2004 «ЮНИ-центр XXI». | |