 |
ЗАДАЧИ ДЛЯ ИССЛЕДОВАНИЯ
Некоторые замечания к списку задач:
- Этот список составлен по материалам различных сборников (в частности, сборника
задач-монстров А.Белова (ДНТТМ, г. Москва), задач Республиканских летних
научно-исследовательских школ учащихся и учителей в п. Лужесно (Витебская
область), турниров юных математиков, олимпиад факультета прикладной математики
и информатики БГУ и т.п.).
- Здесь представлено много задач разных направлений и различного уровня сложности, ряд
из них предназначен для студентов вузов, хотя, возможно, некоторые из
школьников и попытаются ими заняться.
- Обращаем внимание на то, что к любой из этих
задач, вообще говоря, можно и
следует относиться лишь как к источнику идеи: можно решать так, как она
здесь представлена, но можно взяться за отдельные частные случаи, направления,
похожие формулировки и под. Главное начать и получить хотя бы небольшой
результат. Очень часто в исследовании речь не идет о полном решении задачи.
Наоборот, решение исходной постановки должно приводить к уточнению
формулировки, к появлению новых вопросов и т.д.
Телефоны для связи:
209-50-70 (Задворный Борис Валентинович
Электронная почта: zadvorny@bsu.by
| 1. |
Площадь объединения
Какова максимальная площадь объединения N треугольников, вписанных в единичную
окружность? |
| 2. |
Многочлены
Найти все многочлены с натуральными
коэффициентами, обладающие свойством: F(p) – простое при всяком
простом p. |
| 3. |
Сложность 100
С переменной x и действительными числами разрешается провести не
более 100 операций сложения, умножения и возведения в любую натуральную степень.
Можно ли получить многочлен с любым данным числом действительных корней? |
| 4. |
Операции
Можно ли из числа 3 применением операций N
®
N!, N ®
[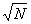 ] получить любое натуральное
число? ] получить любое натуральное
число? |
| 5. |
Сумма
Обозначим через S(y) сумму цифр числа y. Докажите, что существует бесконечно
много номеров N, таких, что S(2N)>S(2N+1). |
| 6. |
Поиск
Один из игроков рисует на плоскости выпуклый N-угольник и записывает координаты
некоторой точки. Второй может проводить произвольную прямую, а первый
сообщает с какой стороны от нее расположена точка. Какое наименьшее число
прямых всегда достаточно, чтобы определить, внутри или снаружи многоугольника
находится точка? |
| 7. |
Заборы
На плоскости отметили N точек и N – 2 непересекающихся отрезка. Докажите, что
найдутся две точки, которые «видят» друг друга (точки не лежат на отрезках). |
| 8. |
Многоугольник
Дан выпуклый K-угольник.
В него вписывают N-угольники, где N<K, T(N)
– наибольшая площадь такого N-угольника. Докажите, что T(N-1)
+T(N+1) не больше 2T(N). |
| 9. |
Ограниченность
Ограничена ли последовательность:
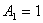 , ,
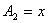 , ,
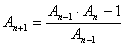 ,
если 1<x<2? ,
если 1<x<2? |
| 10. |
Последовательность
На ленте записана бесконечная последовательность
цифр. Докажите, что либо из нее можно вырезать 10 стозначных чисел, идущих в
порядке убывания, либо какая-нибудь комбинация цифр повторяется 10 раз
подряд. |
| 11. |
Неравенство в целых числах
Докажите, что неравенство 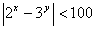 имеет только конечное число решений.
имеет только конечное число решений. |
| 12. |
Целые матрицы
Пусть A,B – целочисленные матрицы.
Известно, что
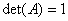 , ,
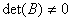 .
Докажите, что существует N, такое, что .
Докажите, что существует N, такое, что
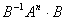
- целочисленная матрица. |
| 13. |
Многочлен
Если функция бесконечно дифференцируема на всей
числовой прямой и в каждой точке имеет только конечное число ненулевых
производных, то она – многочлен. Докажите. |
| 14. |
Функция
Существует ли функция, недифференцируемая во всех
иррациональных точках, и дифференцируемая во всех рациональных? |
| 15. |
Ряд
Пусть V(k) – сходящийся ряд векторов в
пространстве Rn.
Рассмотрим все сходящиеся ряды, полученные перестановкой слагаемых V(k).
Докажите, что множество их сумм есть линейное многообразие.
|
| 16. |
Расстояния
Дан квадрат с вершинами в точках (+-1,+-1). Существует
ли на оси OX точка, расстояния от
которой до всех вершин рациональны? |
| 17. |
Остатки
Последовательность целых чисел 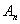 такова, что
такова, что 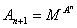 Докажите, что последовательность остатков чисел
Докажите, что последовательность остатков чисел
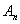 при делении на K стабилизируется.
при делении на K стабилизируется. |
| 18. |
Отрезание
Дан прямоугольник с отношением сторон
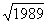 От него отрезают квадрат, а с оставшимся прямоугольником
производят ту же процедуру. Докажите, что последовательность отношений сторон
у построенных прямоугольников периодична.
От него отрезают квадрат, а с оставшимся прямоугольником
производят ту же процедуру. Докажите, что последовательность отношений сторон
у построенных прямоугольников периодична. |
| 19. |
Среднее
Семейство непрерывных функций Fn называется средним,
если оно удовлетворяет
следующим свойствам:
1) Функция Fn
симметрична, однородна,
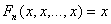 , ,
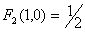
2) Наследственность:
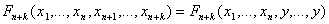 , где
, где 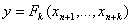 .
Докажите, что функция Fn есть среднее арифметическое. .
Докажите, что функция Fn есть среднее арифметическое. |
| 20. |
Последовательность Туэ
Существует ли бесконечная последовательность из
трех букв, такая, что никакая комбинация из букв не повторится два раза
подряд? | |
| 21. |
Периодические точки
Наличие точки периода 3 под действием непрерывной
на отрезке [0,1] функции F влечет
наличие точек любого периода. Что следует из наличия точки периода 10?
(Период точки – это сколько раз надо к ней применить F, чтобы снова получить ее саму.) |
| 22. |
Расходящийся ряд
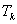 - положительные числа.
Докажите, что ряд
- положительные числа.
Докажите, что ряд
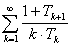 расходится.
расходится. |
| 23. |
Не многочлен
Существует ли бесконечно дифференцируемая функция
от двух переменных 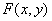 , такая, что при всех
, такая, что при всех
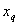 из Q
из Q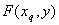 - многочлен от y, при всех
- многочлен от y, при всех 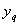 из Q
из Q 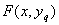 - многочлен от x, а сама функция
- многочлен от x, а сама функция
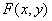 - не многочлен? - не многочлен? |
| 24. |
Степень 5
Найдите такое N,
что в десятичной записи 5n
содержится по крайней мере 1989 нулей. |
| 25. |
Проекции
Докажите, что для любой треугольной пирамиды
найдутся две плоскости, такие, что отношение площадей ортогональных проекций
пирамиды на эти плоскости не меньше корня из двух. |
| 26. |
Вписать кривую
На плоскости отмечено бесконечное множество точек,
никакие три из которых не лежат на одной прямой. Тогда найдется выпуклая
кривая, проходящая через его бесконечное подмножество. Доказать. |
| 27. |
Сумма квадратов
Если многочлен от нескольких переменных всюду
неотрицателен, то он – сумма квадратов рациональных дробей. Доказать. |
| 28. |
Рациональные хорды
Можно ли на окружности радиуса 1 отметить 1985
точек так, чтобы длина любой соединяющей их хорды была рациональным числом? |
| 29. |
Знаки в ряду
В ряд написаны 20 знаков - крестиков и ноликов. Назовем несколько
стоящих подряд крестиков и ноликов симметричной комбинацией, если комбинация
не изменится при отражении относительно некоторой оси. Оцените, какое число
симметричных комбинаций можно найти в любом таком ряду (ответ: не менее
чем…). |
| 30. |
Ломаная
При каких N
и K существует замкнутая N-звенная ломаная, которая пересекает
каждое свое звено ровно K раз? |
| 31. |
Профессор Смит
В квадратном зале с зеркальными стенами стоит
профессор Смит. Он хочет расставить в зале несколько студентов так, чтобы со
своего места он не мог увидеть собственного отражения. Удастся ли профессору
это сделать? |
| 32. |
Многочлен
Дан многочлен P(x) с целыми коэффициентами. Известно,
что P(N)>N при любом
натуральном N, и для любого
натурального L найдется член
последовательности
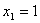 , ,
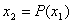 , ... , , ... ,
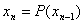 , ...
делящейся на L.
Найдите P(1). , ...
делящейся на L.
Найдите P(1). |
| 33. |
Будет?
Известно, что если зафиксировать одну переменную,
то функция F(x,y) по другой будет
многочленом. Докажите, что она будет сама многочленом от двух переменных. |
| 34. |
Маршруты
Проведите на плоскости прямые и отметьте несколько
точек так, чтобы на любой прямой лежало 4 отмеченных точки и через каждую
отмеченную точку проходило бы ровно 4 прямых. |
| 35. |
Стаканы
У 3 алкоголиков есть бесконечно большие стаканы. В
них натуральное число литров. Один может перелить другому столько, сколько у
того уже есть. Всегда ли они могут перелить всю жидкость в 2 стакана? |
| 36. |
Многогранник
Дан многогранник с 7N гранями. Найдется ли у него N
граней с одинаковым числом вершин? |
| 37. |
Покрытие
Найдите N
треугольников, покрывающих единичную окружность.
а) Наименьшей общей площади;
б) Наименьшей площади объединения. |
| 38. |
Сумма цифр
Докажите, что 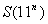 ®
¥
при n
®¥.
®
¥
при n
®¥.
|
| 39. |
Определитель
Существует ли матрица 12x12, составленная из 0, 1, ‑1,
определитель которой равен 1991? |
| 40. |
Эллипс
Докажите, что луч света бегающий в зеркальном
эллипсе касается либо некоторого эллипса, либо некоторой гиперболы. |
| 41. |
Любая комбинация
Число 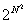 может начинаться с любой комбинацией цифр. Доказать.
может начинаться с любой комбинацией цифр. Доказать. |
| 42. |
Деление круга
Может ли многочлен делящий
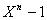 иметь 100 одним из своих коэффициентов? А если он неприводим?
иметь 100 одним из своих коэффициентов? А если он неприводим? |
| 43. |
Ладьи
Какое наименьшее число ладей можно расставить в
кубе NxNxN,
так, чтобы они били все поля? |
| 44. |
Разрезание
Можно ли куб разрезать на части, из которых потом
сложить правильный тетраэдр? |
| 45. |
Прожекторы
На плоскости расположено N точек, в каждой из которых находится прожектор, который
освещает угол 360/N. Докажите, что
эти прожекторы можно развернуть так, чтобы они освещали всю плоскость. |
| 46. |
Без цемента
Из какого минимального количества кирпичей можно
построить башню, так, чтобы смещение нижнего основания относительно верхнего
равнялось 1 км? Длина кирпича 20 см. |
| 47. |
Пятиугольник
Каждая диагональ пятиугольника отсекает
треугольник. Докажите, что сумма площадей треугольников больше площади
пятиугольника. |
| 48. |
Таблица
В таблице 100x100 расставлены числа 0,
1, ‑1. Сумма всех чисел в таблице – 0. Докажите, что найдутся две
строки и два столбца, сумма чисел на пересечении которых равна 0. |
| 49. |
Химики и алхимики
На конгресс собралось 1990 ученых – химиков и
алхимиков. Химик правдив, а алхимик может и соврать. Химиков больше. За какое
минимальное число вопросов можно установить, кто есть кто? |
| 50. |
Нумерация
Существует ли многочлен от двух переменных,
устанавливающий взаимно-однозначное соответствие между натуральными числами и
точками натуральной решетки? Тот же вопрос для пространства. |
| 51. |
Цифры
Докажите, что найдется такое n, что числа 2n и 3n одновременно начинаются с цифр 1000… |
| 52. |
Эволюция полосы
Бесконечная в обе стороны полоса клетчатой бумаги
состоит из черных и белых клеток. Каждую секунду клетка, имеющая четное число
черных соседей становится белой, а имеющая нечетное число черных соседей –
черной. Докажите, что:
а) Если через 2n
секунд исходная раскраска повторится, то она периодична с периодом
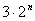
б) Исходная раскраска периодически повторяется
тогда и только тогда, когда она сама периодична (периодичность во времени
равносильна периодичности в пространстве).
в) Что можно сказать о полосе произвольной ширины?
Или о всей клетчатой плоскости? |
| 53. |
Линейный бильярд
а) К квадрату из внешней точки проводится
касательная. Точка отражается относительно точки касания. Через нее
проводится другая касательная и процедура повторяется. Может ли точка убежать
на бесконечность
б) Из точки вне правильного пятиугольника, не
лежащей на продолжении сторон, проводят к нему касательную и точку
симметрично отражают относительно точки касания. С новой точкой происходит то
же, только выбирается другая касательная и т.д. Если мы выйдем на продолжение
стороны, то процесс остановится. Докажите, что найдется бесконечно много
точек периода 10.
в) Что можно сказать в общем случае? (Ориг.
А.Канель). |
| 54. |
Неплоский многоугольник
Для каких K
найдется неплоский правильный K-угольник? |
| 55. |
Стремимся к целому
Число a>1
– алгебраическое иррациональное, но его степень стремится к целому. Тогда оно
единственный корень, по модулю больший 1, некоторого многочлена с целыми
коэффициентами. |
| 56. |
Сумма цифр
При каких K отношение суммы цифр N к сумме цифр KN
ограничено? |
| 57. |
Числитель ряда
Числитель P дроби
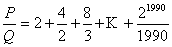 делится на
делится на
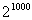 .
Докажите. .
Докажите. |
| 58. |
Число
Может ли число, записываемое одними единицами быть
квадратом целого? А кубом? |
| 59. |
Трубы
Если в городе закрыть 10 насосных станций, то от A к B
вода все равно дойдет.
Докажите, что от A к B по трубам ведет 11
непересекающихся путей. |
| 60. |
Слова
Каждый набор букв – слово гиперруского языка. Одно
слово старше другого, если оно выше стоит в словаре, слово правильное, если
оно старше любой своей циклической перестановки. Докажите, что достаточно
длинное слово содержит подслово вида UXU, где U, X – правильные слова. |
| 61. |
Член не сумма членов
Существует ли последовательность целых чисел,
такая что никакой ее член не есть сумма нескольких других и
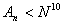 ? ? |
| 62. |
Существует ли?
Существует ли функция на сфере, такая, что если
три точки соответствуют трем взаимно ортогональным векторам, то в одной она
принимает значение 1, а в других – 0? |
| 63. |
Шахматы в пространстве
Могут ли 1000 падей в пространстве заматовать
короля? |
| 64. |
Конец числа
Доказать, что существует бесконечно много N таких, что 2N оканчивает на N.
|
| 65. |
Ровно 4K целых точек
Доказать, что для любого K существует окружность с
центром в начале координат, на которой лежат ровно 4K точек с целыми
координатами. |
| 66. |
Сечение пирамиды
Периметр любого сечения произвольной треугольной
пирамиды не больше периметра хотя бы одной грани. Доказать. |
| 67. |
Общая сторона
Выпуклый четырехугольник разрезан на треугольники.
Доказать, что у двух из них есть общая сторона. |
| 68. |
Фигура
Доказать, что в любую выпуклую фигуру площади 1
можно вписать треугольник площади
а*) 3/8
б**) 3·
Ö3
/4p
|
| 69. |
1000 прямых
Плоскость разрезали вдоль 1000 прямых. Известно,
что никакие две прямые не параллельны, и никакие три прямые не пересекаются в
одной точке. Доказать, что среди полученных кусков плоскости будет не менее
998 треугольников. (А какое может быть наибольшее число треугольников? Попробуйте
получить точное значение или хотя бы оценку.) |
| 70. |
N точек
Доказать, что в единичном квадрате можно
разместить N точек (N>2) так, чтобы любые три
точки определяли треугольник площади не менее чем 1·2Ν2. |
| 71. |
Целая сторона
Прямоугольник разрезан на конечное число
прямоугольников, у каждого прямоугольника есть целая сторона. Докажите, что у
исходного прямоугольника также есть целая сторона. |
| 72. |
D I V - G R A D
Городок DIV-GRAD обладает отличной автобусной
сетью! С каждой остановки можно проехать на любую другую без пересадок.
Каждый маршрут имеет пять остановок, а каждые два маршрута имеют единственную
общую остановку. Сколько же автобусных маршрутов в этом дивном граде?
Нарисуйте карту. |
| 73. |
Множество
Множество содержит 1000 различных элементов.
Каково наибольшее количество его подмножеств, попарно несравнимых по
включению? |
| 74. |
Ограниченность
В каждой клетке бесконечного листа бумаги написано
число, причем каждое равно среднему арифметическому четырех своих соседей.
Все числа ограничены. Равны ли они? А если числа написаны в клетках
пространственной решетки? |
| 75. |
Квадраты
Могут ли 4 квадрата целых чисел образовать
арифметическую прогрессию? |
| 76. |
Числа в клеткаx
а) В клетках решетки записаны целые числа. Тогда
найдется квадрат, сумма чисел внутри которого делится на 1990.
б) Если записаны просто числа, то найдется
квадрат, сумма чисел внутри которого сколь угодно близка к целому числу. |
| 77. |
Ряд
Известно, что при любых действительных А, В ряд
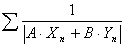 расходится. Обязан
ли расходиться ряд
расходится. Обязан
ли расходиться ряд 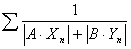 ? А что если А и В могут быть комплексными.
? А что если А и В могут быть комплексными. |
| 78. |
Супершахматы
Эта игра ведется на доске размером 100 на 100 и в
ней участвует 20 различных фигур, каждая из которых ходит по своим правилам.
Известно, что любая фигура с любого места бьет не более 20 полей (но больше о
правилах ничего не сказано, например, если фигуру А передвинуть, то о том, как изменится множество битых полей, мы
ничего не знает). Докажите, что можно расставить на доске все 20 фигур так,
чтобы ни одна из них не била другую. |
| 79. |
Цепочки
Квадрат разбит на прямоугольники.
"Цепочкой" называется такое подмножество К множества этих прямоугольников, что существует сторона квадрата
А, целиком закрытая проекциями
прямоугольников из К, но при этом
ни в какую точку А не проектируются
внутренние точки двух прямоугольников из К.
Докажите, что любые два прямоугольника разбиения входят в некоторую цепочку.
Аналогичная задача для куба, разбитого на прямоугольные параллелепипеды (в
определении цепочки нужно заменить сторону на ребро). |
| 80. |
Степени двойки
Среди значений, принимаемых многочленом Р(Х) при натуральных значениях
аргумента, встречаются все степени двойки. Докажите, что степень многочлена
равна единице. |
| 81. |
Построение
Построить четырехугольник по сторонам и расстоянию
между серединами диагоналей. |
| 82. |
Крестики – нолики
На бесконечном листе клетчатой бумаги двое играют
в такую игру: первый ставит сто крестиков, второй - один нулик. Могут ли
нулики добиться того, чтобы в вершинах хоть - какого то квадрата стояли одни
нулики? |
| 83. |
Деревья
Сколько существует деревьев, соединяющих К точек? |
| 84. |
Отметить вершины
Каждая сторона правильного треугольника разделена
на 30 равных частей. Прямые, проведенные через точки деления, параллельно
сторонам треугольника, разбивают его на 900 маленьких треугольничков. Каково
максимальное число вершин разбиения, никакие две из которых не лежат на
проведенной прямой или стороне? |
| 85. |
Вокруг Коши (А. Беренштейн)
А1
- среднее арифметическое
набора чисел, А2 - средне
геометрическое, М -среднее
арифметическое их кубических корней, D1 - средний квадрат уклонения
величин от А1, D2 - средний квадрат
уклонений кубических корней величин от М.
Докажите неравенства: а)
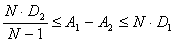
б) при 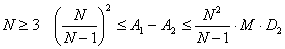 . . |
| 86. |
Вычеркивание
Все ХN и YM - целые. X1 + … + XN
= Y1 + … YM < M × N
тогда в этом равенстве можно вычеркнуть часть слагаемых так, чтобы оно
осталось верным. |
| 87. |
Коммутирующие многочлены
Найдите все многочлены P(X) и Q(X) такие, что P(Q(X)) = Q(P(X)) |
| 88. |
Равномерно отметить
На прямой по порядку расположены точки A1,…, AN так,
что длины всех отрезков [A1A
2], … , [AN-1AN] меньше 1. Можно ли отметить К-1
из точек A1,…, AN так, что бы длины любых двух
частей, на которые разбиваются на
отрезок [A1AN] красными точками отличались
не более чем на 1. |
| 89. |
Приближения
a - иррациональное число, а
b - произвольное из
интервала (0, 1). Q(M) есть
минимум дробной части N×a , где N<M
- целое. Аналогично, R(M) есть минимум дробные части b - N×a. Докажите,
что при бесконечно многих M Q(M)>R(M). |
| 90. |
Монотонная функция
Если функция F монотонна, то она дифференцируема
в некоторой точке. Доказать. |
| 91. |
Жуки
На шахматной доске 99x99 сидят жуки. В кокой-то
момент они полетели и сели снова на доску так, что жуки из соседних
клеток сели либо на соседние, либо на
одну. Обязательно ли какой-то жук сел на исходную клетку, либо соседнюю с
ней. |
| 92. |
Десант
На маленьком острове стоит прожектор, луч которого
освещает отрезок поверхности моря 1 км. Прожектор равномерно вращается с
постоянной угловой скоростью. Какова минимальная скорость катера, чтобы он
смог подойти к острову незамеченным? |
| 93. |
Неравенство
Докажите, что для любого набора положительных
чисел выполнено неравенство:
A1 / (A2 + A3) + A2
/ (A3 + A4) + … + An / ( A1
+ A2) > N
× 1/4.
Можно ли 1/4 заменить большим числом? |
| 94. |
N - универсальность
Дано натуральное число N . Последовательность натуральных чисел
A1,…, AN называется N - универсальной,
если из нее вычеркиванием части членов можно
получить любую перестановку из N чисел.
Например: последовательность 1, 2, 3, 1, 2, 1, 3, является 3-универсальной.
Попробуйте найти возможно более короткую N -универсальную последовательность.(Известны
конструкции такой последовательности длины N2-2N+ 4.) |
| 95. |
Числа на окружности
На окружности расположено N чисел, одно из них равно
1, а сумма всех - ноль. При каком D
должно найтись число, отличающееся от среднего арифметического своих соседей
не более чем на D / N ? |
| 96. |
Функция на сфере
На единичной сфере задана функция такая, что сумма
ее значений на концах трех взаимно-перпендикулярных радиусов равна единице.
Докажите, что эта функция есть квадрат проекции на некоторую ось. |
| 97. |
Билеты и ящики
Имеется 1000 билетов с номерами 000, … , 999 и 100
ящиков с номерами 00, … , 99. Билет разрешается опускать в ящик, если его
номер получается из номера ящика вычеркиванием одной из цифр. В какое наименьшее
число ящиков можно положить билеты? Каков минимальный набор ящиков для
К - значных билетов? |
| 98. |
Взвешивания (четыре цикла задач).
Примечание В задачах (I), (II), (III)
фальшивые монеты весят между собой одинаково, но отличаются от настоящих
по весу.
(I).
а) Из 103 монет 2 фальшивые. Как за три взвешивания на чашечных весах без
гирь определить легче фальшивые монеты настоящих или тяжелее? Чем от этого
случая будут отличаться случаи, когда общее количество монет — 102, 104, 12, 1002? Исследуйте случай
произвольного числа N монет, из которых
две фальшивые.
б) Общая постановка: из N монет K фальшивых (K< N/2).
За сколько взвешиваний на чашечных весах без гирь можно определить легче
фальшивые настоящих или тяжелее?
(II).
а) Из 6 монет 2 фальшивые, про которые известно, что они легче
настоящих. За три взвешивания на чашечных весах без гирь определить все
фальшивые монеты.
б) Общая постановка: из N монет K фальшивых
(K<N/2), которые легче настоящих.
Необходимо определить все фальшивые монеты. Какое минимальное количество
взвешиваний на чашечных весах без гирь вам для этого потребуется?
(III).
Из N монет K фальшивых (K<N/2). Необходимо
определить все фальшивые монеты и одновременно узнать, легче они или тяжелее
настоящих. Какое минимальное количество взвешиваний на чашечных весах без
гирь вам для этого потребуется?
(III).
Имеется по n шариков красного, синего и зеленого цветов.
Все шарики одного цвета имеют
разный вес, причем для любого из шариков имеется еще два шарика такого же
веса других цветов. С помощью чашечных весов без гирь нужно упорядочить по
весу шарики каждого цвета. Докажите, что это можно сделать:
1) за два взвешивания при n = 2;
2) за семь взвешиваний при n = 3;
3) за 22 взвешивания при n = 5;
Попробуйте улучшить эти результаты, а также получить их аналоги для других значений n
. |
| 99. |
Рациональные точки на окружности (кривой второго порядка).
1) Получите критерии (необходимые и достаточные условия) существования
на окружности двух (одной) рациональных точек (т.е. точек (x,y ) обе координаты
рациональны), а также критерии отсутствия таких точек на окружности.
Аналогичные вопросы для кривых второго порядка, задаваемых в общем случае
уравнением:
F(x,y)= ax2 + bxy + cy2 + dx + ey + f = 0.
2) Интересно во всех указанных случаях
проследить, какие различия накладывают на полученные критерии типы кривых,
например, парабола, гипербола, эллипс, две пересекающиеся прямые и т.д.
Например, пусть M
множество точек (x,y), удовлетворяющих уравнению (1), где
a, b, c, d , e, fÎQ,
причем
F(x,y) = (a1x + b1 y + c1
)(a2x + b2y + c2),
где ai,
bi, ci Î R.
Пусть множество M содержит ровно n рациональных точек.
Какие значения может принимать n?
Укажите соответствующие критерии.
3) Получите критерии существования на
кривых второго порядка ровно n точек вида
a + b 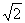 a, bÎQ,
n – натуральное число
или нуль.
a, bÎQ,
n – натуральное число
или нуль.
Примечание. Подробнее см. пункты 4°,5° в статье “На
пути к третьему республиканскому турниру юных математиков“ в журнале
«Матэматыка: праблемы выкладання», 1998, № 4). |
|
100.
|
Максимумы и минимумы плоских выпуклых фигур.
Рассматриваются следующие
величины плоских выпуклых фигур: D
- диаметр плоской выпуклой фигуры Ф,
D - ширина плоской выпуклой фигуры Ф, S - площадь, L - периметр.
а) Найти наибольшее и
наименьшее значение, которое может принимать одна из величин D, D, S, L при условии, что
некоторая другая из них имеет наперед заданное постоянное значение.
б) Найти наибольшее и
наименьшее значение, которое может принимать одна из величин D, D, S, L при условии, что
некоторые другие из них (две или три) имеют наперед заданное постоянное
значение.
в) Обобщите эти понятия и
задачи для пространственных фигур.
Примечание. 1) Исследования можно
начинать для известных школьных выпуклых фигур.
2) Диаметр D - наибольшее возможное
расстояние между точками плоской выпуклой фигуры. Прямая называется опорной
прямой фигуры Ф, если она проходит
хотя бы через одну точку фигуры и вся фигура расположена по одну сторону от
прямой . Шириной D ограниченной выпуклой
фигуры называют наименьшее возможное расстояние между двумя ее параллельными
опорными прямыми.
Литература. Яглом И.М., Болтянский В.Г. Выпуклые фигуры. М., 1951.
|
| 101. | Симметрия в алгебре.
Симметрические и антисимметрические многочлены, их теория, ее развитие и применение
к решению школьных задач.
Литература. Болтянский В.Г., Виленкин Н.Я. Симметрия в алгебре. М., 1967. |
| 102. | Трансверсаль-2.
Трансверсалью называют
любую прямую, пересекающую стороны или продолжения сторон заданного
треугольника (см. [1]). Доказать, что:
1) для каждого из четырех получившихся треугольников существует одна
вписанная и три вневписанные окружности, что дает всего шестнадцать окружностей;
2) центры этих шестнадцати окружностей лежат по четыре на восьми новых
окружностях;
3) эти восемь новых окружностей разделяются на две группы так, что
каждая из четырех окружностей одной группы пересекает ортогонально все
окружности другой группы;
4) центры окружностей обеих групп лежат на двух взаимно перпендикулярных
прямых;
5) эти две последние прямые пересекаются в точке Микеля.
Может быть, вам удастся установить другие интересные факты, относящиеся к данной
конфигурации. Попробуйте обобщить такую конфигурацию на пространство и
получить там соответствующие результаты.
Литература. Борисенко Е., Шевченко Е., Пименов А. Трансверсали // Материалы
Второй республиканской летней научно-исследовательской школы учащихся и
учителей. Минск, 1996, с. 118-119 |
| 103. |
Необычные разрезания.
1) Для каких значений n
вы сможете разрезать выпуклый n-угольник
на трапеции?
2)Верно ли, что любой выпуклый n-угольник можно разрезать на n - 2 трапеции?
3) Возможно, для некоторыхn
вам удастся разрезать произвольный -угольник
на меньшее число трапеций?
4) Дальнейшие направления исследования: а) Для каждого значения n
получить наименьшее число, на
которое можно разрезать произвольный выпуклый -угольник;
б) Рассмотреть интересные (?!) частные случаи
многоугольников; в) Рассмотреть невыпуклые многоугольники.
5) Попробуйте придумать и исследовать другие интересные разрезания
фигур на плоскости и в пространстве. |
| 104. |
Функциональные уравнения с дробно-линейной функцией.
Найти все действительные
числа a, b, c,d
при которых все функции f(x), удовлетворяющие
соотношению f(x+1)=af(x)+b)/(cf(x)+d), являются периодическими.
Исследовать
последовательности вида fn+1=(afn+b)/(cfn+d) на периодичность, ограниченность и монотонность
в зависимости от значений параметров a, b, c, d и первого члена f
1. |
| 105 | Монотонные квадратные числа
Найти все (или как можно
больше) “монотонные квадратные” числа, т.е. числа, которые являются точными
квадратами и цифры которых образуют монотонную последовательность, например:
16, 1156, 111556, 441. |
| 106. |
Симметричные квадратные числа
Найти все (или как можно больше) “симметричные
квадратные” числа, т.е. числа, которые являются точными квадратами и читаются
слева направо и справа налево одинаково, например: 121, 484. |
| 107. |
Архимедовы треугольники
Треугольник называется
архимедовым по отношению к параболе, если последняя касается двух сторон
треугольника в его вершинах.
Рассмотрим треугольник,
который является архимедовым по отношению к трем параболам. Докажите или
опровергните гипотезу: фокальный треугольник, т.е. треугольник, вершинами
которого являются фокусы этих парабол, подобен исходному [2*,c.25-27]. |
| 108. | Антимагические квадраты
Антимагические квадраты порядка n - это квадраты, содержащие n
2 натуральных
чисел, так, что суммы чисел на всех горизонталях, вертикалях и двух главных
диагоналях различны (в отличие от магических квадратов). В [1-3, см. список
литературы ниже] введено понятие антимагических квадратов первого и второго
рода. В [3] получены ответы на два первых принципиальных вопроса (можно
сказать, локального характера) - о существовании антимагических квадратов
первого и второго рода различных порядков и способе их построения. Сразу за
ними встают два следующих принципиальных вопроса (по существу, глобальных) -
1) сколько существует антимагических квадратов каждого порядка n
; 2) найти алгоритм, позволяющий найти все
такие квадраты. Одновременно встает множество вопросов, открывающих другие
направления в этой проблеме [3].
Литература. Акулич И. Антимагические квадраты //Фокус, 1994,
№ 2.
Федоров И. Еще раз об антимагических квадратах //Фокус, 1995, № 3.
Ваннэ Ю. Антимагические квадраты.//«Репетитор» |
| 109. | Карты
Возьмем колоду из k(k >=4) карт, перемешанных каким-то образом:
a1, ..., ak.
После этого разложим все карты по порядку в ряд: a1, ..., ak.
За каждый шаг мы будем выбирать минимальное i (i Î N, i < k - 1) такое, что ai = ai+2
(если такое i существует) и
выкидывать карту из ряда, сокращая тем самым ряд на одну карту. Мы сможем
совершить лишь конечное число таких ходов, после чего получим “несокращаемый”
ряд: b1, ... , bc. Перетасуем этот ряд
следующим образом: b1, b3, ... , b2,
b4, ... (сначала упорядочено идут карты с нечетными индексами, а после - с
четными). С полученным теперь рядом проделаем ту же операцию, что мы
проделали с рядом: a1,
..., ak . и т. д.
Подобные операции будем проделывать до тех пор, пока в ряду не останется 2
карты.
Какова вероятность того, что мы сделали это
за n операций? Попробуйте
решить аналогичную задачу для других способов тасования. |
| 110. | Перекрашивания кругами
На белую клетчатую
плоскость последовательно помещаются круги: w1,
w1, ... , wn ,
радиусы которых
равны r1, r2, ... , rn соответственно, после
чего плоскость
перекрашивается следующим образом: любая точка (не клетка!), которую
покрывает четное число кругов остается белой, все остальные точки становятся
черными. В результате таких действий мы выделяем на нашей плоскости некоторую
черную фигуру F площадью S,
которая покрывает с узлов нашей плоскости. Исследуйте зависимость чисел F
и c от чисел n, r1, r2, ... , rn.Попробуйте решить аналогичную задачу для
квадратов и правильных треугольников. |
| 111. | Последовательности из модулей
Последовательность (an) натуральных чисел a
0, a1, a2, a3, … составляется по
следующему рекуррентному закону:
a0, a1, an+1 = |an - an-1
| (a0 и a1
заданы).
Продолжается последовательность до первого нуля.
1) Известно, что каждое
число, входящее в последовательность, не превосходит 1998. Какое наибольшее
количество членов может содержать такая последовательность?
Изучите свойства
последовательности (an для случаев:
2) рациональных чисел,
3) любых действительных
чисел,
4) последовательность (an строится по правилу a0, a1, an+1 =
|an - ban-1| (a0, a1 и b заданы; члены
последовательности, как и в случаях 1), 2), 3), являются натуральными,
рациональными либо действительными числами).
Попробуйте получить общие
условия на a0 и a1, обеспечивающие
конечность указанных последовательностей, и оценить количество их членов в
этих случаях. |
| 112. |
Исследование диофантового уравнения
Предложите метод (методы)
решения в целых числах уравнений вида
x3+30xy+y3 = M,
где M -
целое число. В частности, получите решения этого уравнения при M = 1998 и
M = 1999. |
| 113. |
Отображения множеств
Пусть Х - множество с n
элементами, где n ³ 2, Р - совокупность всех
подмножеств множества Х; Y - множество с mэлементами, m ³ 1. Докажите, что
следующие утверждения эквивалентны:
(а) m £ n;
(b) для любого отображения f:P ® Y,
найдутся такие А и В из Р, что
f(A) = f(B) = f(AÈB) = f(AÇB). |
| 114. |
Странное умножение.
Найдите как можно больше
пар натуральных чисел таких, что результат их умножения выражен цифрами
одного из сомножителей, разделенными одним или несколькими нулями. Например,
126*81=10206 , 18*56=1008. |
| 115. |
Тетраэдр в кубе.
Поместите в куб правильный
тетраэдр максимального объема. Не будет ли этот тетраэдр иметь наибольший
объем среди всех тетраэдров, которые можно поместить в куб?
Впишите тетраэдр
наибольшего объема в прямоугольный параллелепипед и в произвольный
параллелепипед.
Как должен располагаться в
параллелепипеде (прямоугольном или произвольном) правильный тетраэдр, чтобы
он имел наибольший объем среди всех таких правильных тетраэдров.
Укажите в каждом случае
соответствующее значение объема тетраэдра в зависимости от длин ребер куба
или параллелепипеда и плоских углов при вершине. |
| 116. |
Задача о количестве острых и тупых углов.
Чему равно
наибольшее число острых углов в плоском (несамопересекающемся) n-угольнике? А
чему может быть равно наименьшее число тупых углов?
Примечания. Для второго вопроса возможно
рассмотрение двух случаев: а) величина тупого угла лежит в интервале (90°
;180° ), б) величина тупого угла лежит в интервале (90°
; 360°). Изменятся ли ответы во всех случаях, если вместе с
острыми или соответственно тупыми углами рассматривать прямые углы? |
| 117. |
Равнобедренные достроения
Треугольник АВС равносторонний. Найдите
все такие точки М, что треугольники МАВ, МАС и МВС равнобедренные.
АВСD - квадрат. Найдите все такие точки М,
что треугольники МАВ, МВС, МСD и МDA - равнобедренные.
Исследуйте аналогичные
задачи для других правильных (а может, и не только правильных)
многоугольников. Возможно, вы найдете в этих задачах какие-либо общие закономерности. |
| 118. | Цифровая структура чисел в арифметической прогрессии
1) Докажите, что в любой бесконечной арифметической прогрессии (т.е.
содержащей бесконечное число членов) найдется член, в десятичной записи
которого есть хотя бы одна цифра 0.
2) Обозначим через L длину (количество членов) некоторой арифметической прогрессии.
Для какого
наибольшего значения L
вы сможете построить пример арифметической прогрессии длины L,
такой, что десятичная
запись ни одного ее члена не содержит нулей? (Возможно, здесь вы укажете
конкретный пример, или способ построения, или доказательство существования
соответствующей прогрессии и т.п.)
3) Останутся ли справедливыми утверждения пп. 1) и 2), если вместо цифры
0 взять какую-либо другую цифру к
(1 £ к £ 9)?
Сформулируйте гипотезы, аналогичные полученным в
пп. 1) и 2), и, по возможности, проверьте их истинность для такого случая: в
десятичной записи членов арифметической прогрессии ищется не отдельная цифра,
а вполне определенная комбинация последовательно расположенных цифр
(например, в числе 5123648 есть комбинация «123»). |
| 119. |
Удивительные фигуры на координатной плоскости
Попробуйте изобразить на координатной плоскости
хотя бы одну фигуру G,
любые две точки которой M(x1y1) и N(x2y2)
удовлетворяют условию:
ê x1y2 - x2y1÷ £ 1999.
Вопросы для исследования.
1) Изучите характер
расположения таких фигур (т.е. фигур, удовлетворяющих указанному выше
условию) на плоскости, а также возможность «увеличения» любой такой фигуры
(т.е. насколько вам удастся максимизировать размеры фигур).
2) Что вы можете сказать о формах таких фигур и их свойствах
(выпуклость, размеры, возможность отображения друг в друга и др.)? |
| 120. |
Разрезания на подобные фигуры
a) Найдите все натуральные
числа n, при которых квадрат можно разрезать на n не обязательно равных
квадратов.
б) Найдите все натуральные
числа n, при которых равносторонний треугольник можно
разрезать на n не обязательно равных
равносторонних треугольников.
в) Найдите как можно больше значений n,
при которых куб можно разрезать на n не обязательно равных кубов. |
| 121. |
Расстановки чисел в таблице
а) В квадратной таблице n x n расставьте числа 1, 2, …, n
2 так, чтобы разность между любыми соседними числами не превосходилаn.
(Два числа в таблице называются соседними, если они стоят в клетках,
которые имеют общую сторону).
б) Докажите, что при любой расстановке чисел в такой таблице найдутся два
соседних числа, разность
которых не меньше n.
в) Сформулируйте и докажите утверждения,
аналогичные пунктам а) и б), хотя бы для одного из случаев:
(I) В прямоугольной таблице m x n расставлены числа
1,2,…, mn;
(II) В кубе n x n x n единиц, разбитом на
n3 единичных кубиков,
расставлены числа 1, 2,…, n3. |
| 122. |
Восстановление осей координат и восстановление функций
На плоскости имеется график функции y=f(x).
Незнайка стер оси координат, отрезок единичной
длины и весь график за исключением некоторого маленького участка. Можно ли
восстановить оси координат и единичный отрезок, а также другие точки графика
в следующих случаях:
1) y = x2;
2) y = 2x;
3) y = 1/x;
4) F(x,y)= ax2
+ 2bxy + cy2 + dx + ey + f = 0;
и других.
Общая задача: описать по возможности
более широкий класс функций, для которых эта задача разрешима. |
|
 |



